b) Chứng minh rằng AA'.AA' = A'M.A'B.. Câu 73 trang 113 Sách Bài Tập (SBT) Toán 9 Tập 2 - Bài tập ôn chương III - Góc với đường tròn
Cho đường tròn đường kính AB. Qua A và B kẻ hai tiếp tuyến của đường tròn đó. Gọi M là một điểm trên đường tròn. Các đường thẳng AM và BM cắt các tiếp tuyến trên lần lượt tại B’ và A’.
a) Chứng minh rằng \({\rm{AA}}’.BB’ = A{B^2}\)
b) Chứng minh rằng \(A'{A^2} = A’M.A’B\).
Giải
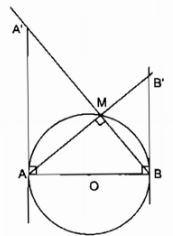
a) Xét ∆AA’B và ∆BB’A:
\(\widehat {A’AB} = \widehat {B’BA} = {90^0}\)
Advertisements (Quảng cáo)
\(\widehat {BB’A} = \widehat {ABA’}\) (vì cùng phụ với \(\widehat {BAB’}\))
Suy ra: ∆AA’B đồng dạng ∆BAB’ (g.g)
\({{AA’} \over {BA}} = {{AB} \over {BB}} \Rightarrow AA’.BB’ = A{B^2}\)
b) \(\widehat {AMB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow AM \bot A’B\)
∆AA’B vuông tại A. Theo hệ thức lượng trong tam giác vuông ta có:
\(AA{‘^2} = A’M.A’B\)