Cho lục giác ABCDEF. Chứng minh rằng đường chéo BF chia AD thành hai đoạn thẳng theo tỉ số 1: 3.
Giải
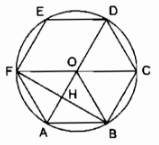
Lục giác đều ABCDEF nội tiếp trong đường tròn (O)
\(\overparen{AB}\) = \(\overparen{CB}\) = \(\overparen{CD}\) = \(\overparen{DE}\) = \(\overparen{EF}\) = \(\overparen{FA}\) = 600
\( \Rightarrow \) sđ \(\overparen{ABCD}\) = sđ \(\overparen{AB}\) + sđ \(\overparen{BC}\) + sđ \(\overparen{CD}\) = 1800
Nên AD là đường kính của đường tròn (O)
Advertisements (Quảng cáo)
Ta có: OA = OB = OF = AB = AF = R
Nên tứ giác ABOF là hình thoi
Gọi giao điểm của AD và BF là H
Ta có: \(FB \bot OA\) (tính chất hình thoi)
\( \Rightarrow AH = HO = {{AO} \over 2} = {R \over 2}\)
\(HD = HO + OD = {R \over 2} + R = {{3R} \over 2}\)
Suy ra: \({{AH} \over {HD}} = {{{R \over 2}} \over {{{3R} \over 2}}} = {1 \over 3}\)
