
Cho tam giác ABC. Vẽ đường tròn (O) đi qua B và C và tâm đường tròn nằm trên AC. Khi nào thì tâm đường tròn (O) trùng với điểm A?
+) Chứng minh điểm \(O\) thuộc trung trực của \(BC\), dựa vào giả thiết suy ra cách dựng điểm \(O\).
+) Chứng minh khi \(O \equiv A\) thì \(A\) thuộc trung trực của \(BC\), từ đó suy ra tính chất của tam giác \(ABC\).

Advertisements (Quảng cáo)
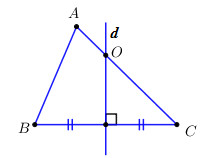
Do \(B,C \in \left( O \right) \Rightarrow OB = OC \Rightarrow \) Điểm \(O\) thuộc trung trực của \(BC\).
Gọi \(d\) là đường trung trực của đoạn thẳng \(BC \Rightarrow O \in d\).
Lại có \(O \in AC\,\,\left( {gt} \right) \Rightarrow O = d \cap AC\).
Khi \(O \equiv A \Rightarrow A \in d \Rightarrow AB = AC\), khi đó tam giác \(ABC\) trở thành tam giác cân tại \(A\).
Vậy điều kiện để \(O \equiv A\) là tam giác \(ABC\) là tam giác cân tại \(A\).
Baitapsgk.com
