
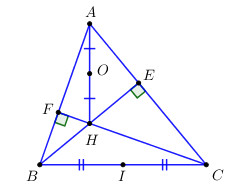
Cho tam giác ABC nhọn, hai đường cao BE và CF cắt nhau tại H.
a) Chứng minh ràng bốn điểm B, F, E, C cùng thuộc một đường tròn.
b) Gọi O là trung điểm AH. Chứng minh rằng E, F thuộc đường tròn (O;OA).
Dựa vào định lí đường trung tuyến trong tam giác vuông: Trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.

Advertisements (Quảng cáo)
a) Gọi \(I\) là trung điểm của \(BC\).
Ta có \(\Delta BFC\) vuông tại \(F \Rightarrow IF = \dfrac{1}{2}BC = IB = IC\,\,\left( 1 \right)\) (trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
\(\Delta BEC\) vuông tại \(E \Rightarrow IE = \dfrac{1}{2}BC = IB = IC\,\,\left( 2 \right)\) (trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
Từ (1) và (2) \( \Rightarrow IE = IF = IB = IC \Rightarrow \) bốn điểm \(B,\,\,F,\,\,E,\,\,C\) cùng thuộc đường tròn tâm \(I\) đường kính \(BC\).
b) Ta có:
\(\Delta AEH\) vuông tại \(E \Rightarrow OE = \dfrac{1}{2}AH = OA = OH\,\,\,\left( 3 \right)\) (trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
\(\Delta AFH\) vuông tại \(F \Rightarrow OF = \dfrac{1}{2}AH = OA = OH\,\,\left( 4 \right)\) (trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
Từ (3) và (4) \( \Rightarrow OE = OF = OA = OH \Rightarrow \) bốn điểm \(A,\,\,F,\,\,E,\,\,H\) cùng thuộc đường tròn tâm \(O\) đường kính \(AH\).
Vậy \(E,F \in \left( {O;OA} \right)\).
Baitapsgk.com
