
Cho hình thang cân ABCD ( AB // CD). Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Xác định tâm O của đường tròn này.
Gọi \(O\) là giao điểm của trục của hình thang cân \(ABCD\) và đường trung trực của cạnh bên \(AD\). Sử dụng tính chất: Điểm thuộc trung trực của một đoạn thẳng cách đều 2 đầu mút của đoạn thẳng đó chứng minh \(OA = OB = OC = OD\).

Advertisements (Quảng cáo)
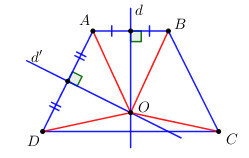
Gọi \(d\) là trục của hình thang cân \(ABCD\), \(d’\) là đường trung trực của cạnh bên \(AD\).
Gọi \(O = d \cap d’\) ta có:
\(d\) là trục của hình thang cân \(ABCD \Rightarrow d\) là đường trung trực của AB và CD.
Mà \(O \in d \Rightarrow \left\{ \begin{array}{l}OA = OB\\OC = OD\end{array} \right.\,\,\left( 1 \right)\) (điểm thuộc trung trực của một đoạn thẳng cách đều 2 đầu mút của đoạn thẳng đó).
Lại có \(O \in d’ \Rightarrow OA = OD\,\,\left( 2 \right)\) (điểm thuộc trung trực của một đoạn thẳng cách đều 2 đầu mút của đoạn thẳng đó).
Từ (1) và (2) \( \Rightarrow OA = OB = OC = OD\).
Vậy bốn điểm \(A,\,\,B,\,\,C,\,\,D\) cùng thuộc đường tròn tâm \(O\), bán kính \(R = OA = OB = OC = OD\).
Baitapsgk.com
