
Cho hình vuông ABCD.
a) Chứng minh rằng bốn đỉnh hình vuông nằm trên một đường tròn. Hãy chỉ rõ tâm của đường tròn đó.
b) Tính bán kính của đường tròn, biết cạnh hình vuông là 4 cm.
+) Dựa vào tính chất: Hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
+) Áp dụng định lí Pytago để tính được bán kính.
Advertisements (Quảng cáo)

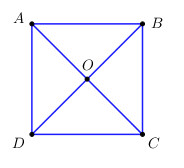
a) Gọi \(O = AC \cap BD\).
Do \(ABCD\) là vuông, do đó hai đường chéo \(AC\) và \(BD\) bằng nhau và cắt nhau tại trung điểm mỗi đường \( \Rightarrow OA = OB = OC = OD\).
Vậy bốn điểm \(A,\,\,B,\,\,C,\,\,D\) cùng thuộc đường tròn tâm \(O\), bán kính \(R = OA = OB = OC = OD\).
b) Áp dụng định lí Pytago trong tam giác vuông \(OAB\) ta có:
\(\begin{array}{l}O{A^2} + O{B^2} = A{B^2}\\ \Leftrightarrow O{A^2} + O{B^2} = A{B^2}\\ \Leftrightarrow 2O{A^2} = {4^2} = 16\\ \Leftrightarrow O{A^2} = 8\\ \Leftrightarrow OA = 2\sqrt 2 \,\,\left( {cm} \right)\end{array}\).
Vậy \(R = OA = 2\sqrt 2 \,\,\left( {cm} \right)\).
Baitapsgk.com
