
Cho lục giác lồi ABCDEF có các đỉnh nằm trên một đường tròn và có hai cặp cạnh đối song song AB // DE, BC // EF. Chứng minh rằng cặp cạnh đối còn lại cũng song song với nhau.
+) Gọi H, K, M, N, P, Q lần lượt là trung điểm của AB, DE BC, EF, AF, CD.
+) Chứng minh O; H; K thẳng hàng, O; M; N thẳng hàng.
+) Chứng minh \(\widehat {AOC} = \widehat {FOD};\,\,\widehat {AOP} = \widehat {FOP};\,\,\widehat {COQ} = \widehat {DOQ} \Rightarrow \widehat {POQ} = {180^0}\) , từ đó suy ra O; P; Q thẳng hàng.
+) Chứng minh AF và CD cùng vuông góc với PQ.

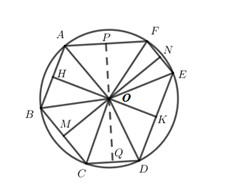
Gọi H, K lần lượt là trung điểm của AB và DE ta có:
\(OH \bot AB;\,\,OK \bot DE\)(quan hệ vuông góc giữa đường kính và dây cung)
Lại có \(AB//DE\,\,\left( {gt} \right) \Rightarrow OH \bot DE\)
Từ O ta có thể kẻ hai đường thẳng OH và OK cùng vuông góc với DE \( \Rightarrow O;H;K\)thẳng hàng.
Advertisements (Quảng cáo)
Gọi M, N lần lượt là trung điểm của BC và EF. Chứng minh tương tự ta có O, M, N thẳng hàng.
\( \Rightarrow \widehat {HOM} = \widehat {NOK}\) (đối đỉnh).
Xét tam giác OAB có \(\left\{ \begin{array}{l}OA = OB = R\\OH \bot AB\end{array} \right. \Rightarrow \widehat {AOH} = \widehat {BOH} = \dfrac{1}{2}\widehat {AOB}\)
Xét tam giác OBC có \(\left\{ \begin{array}{l}OB = OC = R\\OM \bot BC\end{array} \right. \Rightarrow \widehat {BOM} = \widehat {COM} = \dfrac{1}{2}\widehat {BOC}\)
\( \Rightarrow \widehat {AOB} + \widehat {BOC} = 2\widehat {BOH} + 2\widehat {BOM} = 2\widehat {HOM} \Leftrightarrow \widehat {AOC} = 2\widehat {HOM}\)
Chứng minh tương tự ta có \(\widehat {FOD} = 2\widehat {NOK}\)
Mà \(\widehat {HOM} = \widehat {NOK}\,\,\left( {cmt} \right) \Rightarrow \widehat {AOC} = \widehat {FOD}\,\,\left( 1 \right)\).
Gọi P, Q lần lượt là trung điểm của AE và CD.
Tam giác OAF cân tại O \(\left( {OA = OF = R} \right) \Rightarrow OP \bot AF \Rightarrow \) Đường cao OP đồng thời là phân giác \( \Rightarrow \widehat {AOP} = \widehat {FOP}\) (2)
Chứng minh tương tự ta có \(\widehat {COQ} = \widehat {DOQ}\,\,\,\left( 3 \right)\).
Từ (1), (2) và (3) \( \Rightarrow \widehat {AOC} + \widehat {AOP} + \widehat {COQ} = \widehat {FOD} + \widehat {FOP} + \widehat {DOQ} \Rightarrow \widehat {POQ} = {180^0} \Rightarrow O;P;Q\) thẳng hàng.
\( \Rightarrow OP \bot CD\).
Vậy \(AF//CD\) (cùng vuông góc với OP).
