
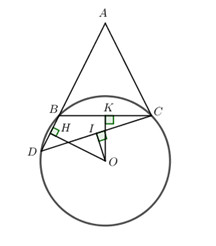
Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D (BD < BC). Vẽ đường tròn tâm O ngoại tiếp tam giác BCD.
a) So sánh các cung DB, BC, DC.
b) Gọi I, H, K lần lượt là hình chiếu vuông góc của O xuống DC, BD và BC. So sánh các đoạn OI, OH, OK.
a) Chứng minh \(\widehat {CBD} > {90^0} \Rightarrow \Delta BCD\) tù \( \Rightarrow \) Cạnh CD là cạnh lớn nhất trong tam giác.
Sử dụng định lí: Dây lớn hơn căng cung lớn hơn.
b) Sử dụng định lí: Dây lớn hơn thì gần tâm hơn.
Advertisements (Quảng cáo)

a) Vì tam giác ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB} < {90^0}\)
Mà \(\widehat {ABC} + \widehat {CBD} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {CBD} > {90^0}\).
Do đó cạnh CD - cạnh đối diện với góc tù là cạnh lớn nhất của tam giác BCD (Trong 1 tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn).
\( \Rightarrow BD < BC < CD \Rightarrow cung\,BD < cung\,BC < cung\,CD\) (dây lớn hơn căng cung lớn hơn).
b) Vì \(BD < BC < CD\) nên \(OH > OK > OI\) (Dây lớn hơn thì gần tâm hơn, dây nhỏ hơn thì xa tâm hơn).
