
Cho tam giác ABC cân tại A và nội tiếp đường tròn tâm O, bán kính R.
a) Chứng minh \(AO \bot BC\) .
b) Giả sử \(AB = R\sqrt 3 \), AO cắt BC tại H và cắt đường tròn O tại I. Chứng minh tam giác ABC đều và tính độ dài AH.
c) Vẽ dây IE // AC, IF // AB (E, F là các điểm trên đường tròn O). Chứng minh tam giác IEF cân.
a) Chứng minh AO là đường trung trực của BC.
b) Chứng minh tam giác ABI vuông, tính độ dài BI, từ đó tính BH.
Chứng minh H là trung điểm của BC \( \Rightarrow BC = 2BH\).
c) Chứng minh \(cung\,AE = cung\,AF \Rightarrow cung\,IE = cung\,IF \Rightarrow IE = IF \Rightarrow \Delta IEF\)

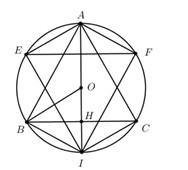
a) Vì tam giác ABC cân tại A\( \Rightarrow AB = AC \Rightarrow A\) thuộc đường trung trực của BC.
Vì \(OB = OC = R \Rightarrow O\) thuộc đường trung trực của BC.
Advertisements (Quảng cáo)
\( \Rightarrow AO\) là trung trực của BC \( \Rightarrow AO \bot BC\).
b) Xét tam giác ABI có \(BO = \dfrac{1}{2}AI \Rightarrow \Delta ABI\) vuông tại B (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
Xét tam giác vuông ABI có: \(B{I^2} = A{I^2} - A{B^2} = {\left( {2R} \right)^2} - {\left( {R\sqrt 3 } \right)^2} - {R^2} \Rightarrow BI = R\) (Định lí Pytago).
Tam giác ABC cân tại A có \(AO \bot BC \Rightarrow AI \bot BC\) tại H và H là trung điểm của BC.
Áp dụng hệ thức lượng trong tam giác vuông ABI có :
\(\dfrac{1}{{B{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{B{I^2}}} = \dfrac{1}{{3{R^2}}} + \dfrac{1}{{{R^2}}} = \dfrac{4}{{3{R^2}}} \Rightarrow BH = \dfrac{{R\sqrt 3 }}{2}\)
Vì H là trung điểm của BC\( \Rightarrow BC = 2BH = R\sqrt 3 \Rightarrow \Delta ABC\) có \(AB = AC = BC = R\sqrt 3 \Rightarrow \Delta ABC\) đều \( \Rightarrow \widehat {ABH} = {60^0}\).
Xét tam giác vuông ABH có : \(AH = AB.\sin {60^0} = R\sqrt 3 .\dfrac{{\sqrt 3 }}{2} = \dfrac{{3R}}{2}\).
c) Ta có \(CO = \dfrac{1}{2}AI \Rightarrow \Delta ACI\)vuông tại C (Trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
Áp dụng định lí Pytago trong tam giác vuông ACI có :
\(CI = \sqrt {A{I^2} - A{C^2}} = \sqrt {{{\left( {2R} \right)}^2} - {{\left( {R\sqrt 3 } \right)}^2}} = \sqrt {{R^2}} = R\)
\( \Rightarrow BI = CI = R \Rightarrow cung\,BI = cung\,CI\)
Vì IE // AC \( \Rightarrow cung\,AE = cung\,CI\). Vì IF // AB \( \Rightarrow cung\,AF = cung\,BI\)
Do đó \(cung\,AE = cung\,AF \Rightarrow cung\,IE = cung\,IF \Rightarrow IE = IF \Rightarrow \Delta IEF\) cân tại I.
