
Cho tam giác ABC vuông ở A có AB = 8, AC = 15. Vẽ đường cao AH. Gọi D là điểm đối xứng với B qua H. Vẽ đường tròn đường kính CD, cắt AC ở E.
a) Chứng minh rằng HE là tiếp tuyến của đường tròn.
b) Tính độ dài HE.
a) +) Gọi \(K\) là trung điểm của \(AE\). Chứng minh \(\Delta AHE\) cân tại H.
+) Chứng minh \(\angle HAE = \angle HEA\), \(\angle IEC = \angle ICE = \angle ACB\), từ đó chứng minh \(\angle HEI = {90^0}\).
b) Áp dụng định lí Pytago và hệ thức lượng trong tam giác vuông tính \(AH\), từ đó tính \(HE\) .

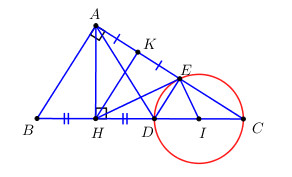
a) Gọi \(I\) là trung điểm của \(CD \Rightarrow I\) là tâm đường tròn đường kính \(CD\).
Xét tam giác \(CDE\) có \(IE = IC = ID = \dfrac{1}{2}CD \Rightarrow \Delta CDE\) vuông tại \(E\).
\( \Rightarrow ED \bot AC\). Mà \(AB \bot AC\,\,\left( {gt} \right) \Rightarrow DE//AB \Rightarrow ABDE\) là hình thang.
Gọi \(K\) là trung điểm của \(AE\). Có \(H\) là trung điểm của \(BD\,\,\left( {gt} \right)\), do đó \(HK\) là đường trung bình của hình thang \(ABDE\).
\( \Rightarrow HK//AB//DE\) \( \Rightarrow HK \bot AC \Rightarrow HK \bot AE\).
Advertisements (Quảng cáo)
Xét \(\Delta AHE\) có \(HK\) là trung tuyến đồng thời là đường cao \( \Rightarrow \Delta AHE\) cân tại \(H\).
\( \Rightarrow \angle HAE = \angle HEA\) (2 góc ở đáy).
Mà \(\angle HAE = \angle ABC\) (cùng phụ với \(\angle BAH\)) \( \Rightarrow \angle ABC = \angle HEA\).
Xét tam giác \(IEC\) có \(IE = IC\) \( \Rightarrow \Delta IEC\) cân tại \(I\).
\( \Rightarrow \angle IEC = \angle ICE = \angle ACB\).
Ta có : \(\angle HEA + \angle HEI + \angle IEC = \angle AEC = {180^0}\)
\(\begin{array}{l} \Rightarrow \angle ABC + \angle HEI + \angle ACB = {180^0}\\ \Rightarrow \angle HEI = {180^0} - \left( {\angle ABC + \angle ACB} \right)\end{array}\).
Mà \(\angle ABC + \angle ACB = {90^0}\) (hai góc nhọn phụ nhau trong tam giác vuông ABC)
\( \Rightarrow \angle HEI = {90^0} \Rightarrow HE \bot IE\). Lại có \(IE\) là bán kính của đường tròn đường kính \(CD\).
Vậy \(HE\) là tiếp tuyến của đường tròn đường kính \(CD\).
b) Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có :
\(B{C^2} = A{B^2} + A{C^2} = {8^2} + {15^2} = 289\) \( \Rightarrow BC = \sqrt {289} = 17\,\,\left( {cm} \right)\).
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) ta có :
\(AH.BC = AB.AC\) \( \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{8.15}}{{17}} = \dfrac{{120}}{{17}}\,\,\left( {cm} \right)\).
Do tam giác AHE cân tại E (cmt) \( \Rightarrow HE = AH = \dfrac{{120}}{{17}}\,\left( {cm} \right)\).
Vậy \(HE = \dfrac{{120}}{{17}}\,\,cm\).
Baitapsgk.com
