
Cho tam giác ABC có hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng bốn điểm A, D, H, E cùng nằm trên một đường tròn (gọi tâm của nó là O).
b) Gọi M là trung điểm của BC. Chứng minh rằng ME là tiếp tuyến của đường tròn (O).
a) Sử dụng định lí : Tam giác vuông là tam giác nội tiếp đường tròn đường kính là cạnh huyền của tam giác vuông đó.
b) Chứng minh \(ME \bot OE\) tại E.

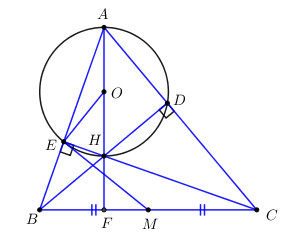
a) Ta có \(CE \bot AB \Rightarrow \widehat {AEH} = {90^0}\)
\(\Rightarrow E\) thuộc đường tròn đường kính AH.
Advertisements (Quảng cáo)
\(BD \bot AC \Rightarrow \widehat {ADH} = {90^0} \Rightarrow D\) thuộc đường tròn đường kính AH.
\( \Rightarrow \) 4 điểm \(A,\,\,D,\,\,H,\,\,E\) cùng thuộc đừng tròn đường kính AH, O là tâm của đường tròn đường kính AH \( \Rightarrow O\) là trung điểm của \(AH\).
b) Kéo dài AH cắt BC tại F. Do H là trực tâm của tam giác ABC \( \Rightarrow AF \bot BC\).
Ta có \(\left\{ \begin{array}{l}\widehat {FAB} + \widehat {ABC} = {90^0}\\\widehat {BCE} + \widehat {ABC} = {90^0}\end{array} \right. \)\(\;\Rightarrow \widehat {FAB} = \widehat {BCE}\) (1).
Lại có : \(\Delta OAE\) cân tại O \(\left( {OA = OE} \right) \Rightarrow \widehat {FAB} = \widehat {OEA}\) (2)
\(\Delta MEC\) cân tại M \(\left( {ME = \dfrac{1}{2}BC = MC} \right)\)\( \Rightarrow \widehat {BCE} = \widehat {MEC}\) (3)
Từ (1), (2) và (3) \( \Rightarrow \widehat {OEA} = \widehat {MEC}\).
Mà \(\widehat {OEA} + \widehat {OEH} = \widehat {AEH} = {90^0}\)
\(\Rightarrow \widehat {MEC} + \widehat {OEH} = {90^0}\)
\(\Rightarrow \widehat {OEM} = {90^0}\).
\( \Rightarrow ME \bot OE\) tại E. Mà OE là bán kính của \(\left( O \right)\).
Vậy ME là tiếp tuyến của \(\left( O \right)\) tại E.
Baitapsgk.com
