
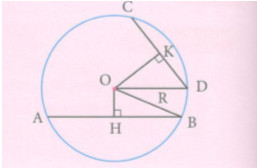
Cho đường tròn (O ; 10 cm) và hai dây AB = 8 cm, CD = 6 cm. Từ O hạ OH và OK theo thứ tự vuông góc với AB và CD.
Hãy tính OH, OK và cho biết đoạn nào dài hơn.

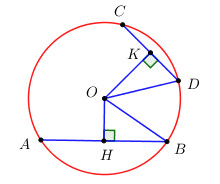
Ta có \(OH \bot AB,\,\,OK \bot CD \Rightarrow \) H, K theo thứ tự là trung điểm của \(AB,\,\,CD\).
\( \Rightarrow HB = \dfrac{1}{2}AB = \dfrac{1}{2}.8 = 4\,\,\left( {cm} \right),\)\(\,\,KD = \dfrac{1}{2}CD = \dfrac{1}{2}.6 = 3\,\,\left( {cm} \right)\)
Áp dụng định lí Pytago trong tam giác vuông \(OHB\) có:
Advertisements (Quảng cáo)
\(O{H^2} = O{B^2} - H{B^2} = {10^2} - {4^2} = 84 \)
\(\Leftrightarrow OH = \sqrt {84} = 2\sqrt {21} \,\,\left( {cm} \right)\)
Áp dụng định lí Pytago trong tam giác vuông \(OKD\) có:
\(O{K^2} = O{D^2} - K{D^2} = {10^2} - {3^2} = 91\)
\(\Leftrightarrow OK = \sqrt {91} \,\,\left( {cm} \right)\)
Do \(91 > 84 \Rightarrow \sqrt {91} > \sqrt {84} \Rightarrow OK > OH\).
Vậy \(OK > OH\).
Baitapsgk.com
