Chu vi hình chữ nhật ABCD là 20cm. Hãy tìm giá trị nhỏ nhất của độ dài đường chéo AC.. Bài 1 trang 134 SGK Toán 9 tập 2 - Phần Hình học - Ôn tập cuối năm - Toán 9
Bài 1. Chu vi hình chữ nhật ABCD là 20cm. Hãy tìm giá trị nhỏ nhất của độ dài đường chéo AC.
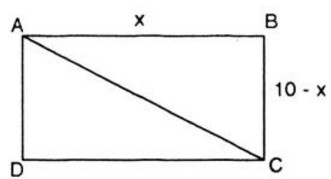
Gọi x (cm) là độ dài cạnh AB (x>0). Theo đề bài thì độ dài cạnh BC là (10 – x)
Advertisements (Quảng cáo)
Áp dụng định lí Py-ta-go trong tam giác vuông ABC, ta có:
\eqalign{ & A{C^2} = A{B^2} + B{C^2} \cr & = {x^2} + {\left( {10 - x} \right)^2} \cr & = 2\left( {{x^2} - 10{\rm{x}} + 50} \right) \cr & = 2\left[ {{{\left( {x - 5} \right)}^2} + 25} \right] \cr & A{C^2} = 2{\left( {x - 5} \right)^2} + 50 \ge 50 \cr}
Đẳng thức xảy ra khi : x – 5 = 0 ⇔ x = 5
Vậy giá trị nhỏ nhất của đường chéo AC là \sqrt50 = 5\sqrt2 (cm)