Bài 2. Tam giác \(ABC\) có góc \(\widehat B = {45^0}\), góc \(\widehat C = {30^0}\). Nếu \(AC = 8\) thì \(AB\) bằng:
(A) \(4\) (B) \(4\sqrt2\)
(C) \(4\sqrt3\) (D) \(4\sqrt6\)
Hãy chọn câu trả lời đúng.

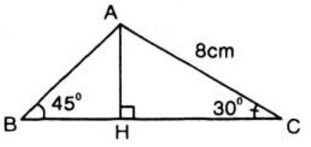
Hạ \(AH \bot BC\) (\(H \in BC\))
Trong tam giác vuông \(HAC\) ( \(\widehat H = {90^0}\) ) có . Vậy \(∆HAC\) là nửa tam giác đều cạnh \(AC\), đường cao \(CH\) cũng là đường trung tuyến.
Advertisements (Quảng cáo)
\(\Rightarrow AH = {{AC} \over 2} = 4(cm)\)
Xét \(∆HAB\) là tam giác vuông cân tại \(H\)
\(⇒ AH = BH = 4\) (\(cm\))
Áp dụng định lí Py-ta-go trong tam giác vuông \(HAB\), ta có:
\(AB = \sqrt {H{A^2} + H{B^2}} = \sqrt {{4^2} + {4^2}} = \sqrt {32} = 4\sqrt 2\)
Vậy \(AB = 4\sqrt2\) \(cm\).
Chọn đáp án B
