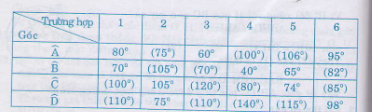
Bài 53. Biết \(ABCD\) là tứ giác nội tiếp. Hãy điền vào ô trống trong bẳng sau (nếu có thể)

Hướng dẫn giải:
- Trường hợp 1:
Ta có \(\widehat{A}\) + \(\widehat{C}\) = \(180^0\) => \(\widehat{C}\) = \(180^0\) - \(\widehat{A}\)= \(180^0\)– \(80^0\)=\(100^0\)
\(\widehat{B}\) + \(\widehat{D}\) = \(180^0\) => \(\widehat{D}\) = \(180^0\) - \(\widehat{B}\)= \(180^0\) – \(70^0\) = \(110^0\)
Vậy điểm \(\widehat{C}\) = \(100^0\) , \(\widehat{D}\) = \(110^0\)
- Trường hợp 2:
Ta có \(\widehat{A}\) + \(\widehat{C}\) = \(180^0\)=> \(\widehat{C}\) = \(180^0\) - \(\widehat{A}\)= \(180^0\)– \(105^0\)= \(75^0\)
\(\widehat{B}\) + \(\widehat{D}\) = \(180^0\) => \(\widehat{D}\) = \(180^0\) - \(\widehat{B}\)= \(180^0\) – \(75^0\) = \(105^0\)
- Trường hợp 3:
Advertisements (Quảng cáo)
\(\widehat{A}\) + \(\widehat{C}\) = \(180^0\)=> \(\widehat{C}\) = \(180^0\)- \(\widehat{A}\)= \(180^0\) – \(60^0\) =\(120^0\)
\(\widehat{B}\) + \(\widehat{D}\) = \(180^0\) Chẳng hạn chọn \(\widehat{B}\)= \(70^0\),\(\widehat{D}\) = \(110^0\)
- Trường hợp 4: \(\widehat{D}\) = \(180^0\)- \(\widehat{B}\)= \(180^0\) – \(40^0\)= \(140^0\)
Còn lại \(\widehat{A}\) + \(\widehat{C}\) = \(180^0\). Chẳng hạn chọn \(\widehat{A}\)= \(100^0\) ,\(\widehat{B}\) =\(80^0\)
- Trường hợp 5: \(\widehat{A}\) = \(180^0\)- \(\widehat{C}\)=\(180^0\) – \(74^0\)= \(106^0\)
\(\widehat{B}\) = \(180^0\) - \(\widehat{D}\)= \(180^0\) – \(65^0\)= \(115^0\)
- Trường hợp 6: \(\widehat{C}\) = \(180^0\) - \(\widehat{A}\)= \(180^0\) – \(95^0\) = \(85^0\)
\(\widehat{B}\) = \(180^0\) - \(\widehat{D}\)=\(180^0\) – \(98^0\) = \(82^0\)
Vậy điền vào ô trống ta được bảng sau: