7. Cho hai phương trình \(2x + y = 4\) và \(3x + 2y = 5\).
a) Tìm nghiệm tổng quát của mỗi phương trình trên.
b) Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong mỗi một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.

a) \(2x{\rm{ }} + {\rm{ }}y{\rm{ }} = {\rm{ }}4{\rm{ }} \Leftrightarrow {\rm{ }}y{\rm{ }} = {\rm{ }} - 2x{\rm{ }} + {\rm{ }}4{\rm{ }} \Leftrightarrow {\rm{ }}x{\rm{ }} = {\rm{ }}-{1 \over 2} y{\rm{ }} + {\rm{ }}2\).
Do đó phương trình có nghiệm dạng tổng quát như sau:
\(\left\{ \matrix{x \in R \hfill \cr y = - 2{\rm{x}} + 4 \hfill \cr} \right.\) hoặc \(\left\{ \matrix{x = - {1 \over 2}y + 2 \hfill \cr y \in R \hfill \cr} \right.\)
\(3x + 2y = 5 \Leftrightarrow y = - {3 \over 2}x + {5 \over 2}\).
Do đó phương trình có nghiệm tổng quát như sau:
\(\left\{ \matrix{
x \in R\hfill \cr
y = - {3 \over 2}x + {5 \over 2} \hfill \cr} \right.\)
b) Vẽ (d1): \(2x + y = 4\)
Advertisements (Quảng cáo)
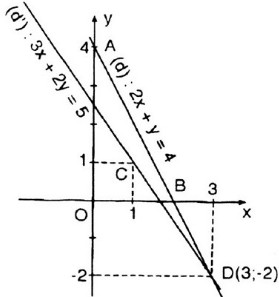
- Cho \(x = 0 \Rightarrow y = 4\) được \(A(0; 4)\).
- Cho \(y = 0 \Rightarrow x = 2\) được \(B(2; 0)\).
Vẽ (d2): \(3x + 2y = 5\)
- Cho \(x = 0 \Rightarrow y = {5 \over 2}\) ,ta được \(M\left( {0;{5 \over 2}} \right)\).
- Cho \(y = 0 \Rightarrow x = {5 \over 3}\) ,ta được \(N \left( {{5 \over 3};0} \right)\).
Hai đường thẳng cắt nhau tại \(D(3; -2)\).
Thay \(x = 3, y = -2\) vào từng phương trình ta được:
\(2 . 3 + (-2) = 4\) và \(3 . 3 + 2 . (-2) = 5\) (thỏa mãn)
Vậy (x = 3; y = -2) là nghiệm chung của các phương trình đã cho.
