Trong tam giác ABC vuông tại A, ta có: \(AB = BC. \cos B\), \(AC = BC. \sin B\). b) + Trong tam giác AHB vuông tại H. Hướng dẫn giải - Bài 1 trang 91 vở thực hành Toán 9 - Bài tập cuối chương IV. Cho tam giác ABC vuông tại A có (widehat B = {60^o}, BC = 20cm). a) Tính AB, AC. b) Kẻ đường cao AH của tam giác. Tính AH, HB, HC...

Cho tam giác ABC vuông tại A có \(\widehat B = {60^o},BC = 20cm\).
a) Tính AB, AC.
b) Kẻ đường cao AH của tam giác. Tính AH, HB, HC.

a) + Trong tam giác ABC vuông tại A, ta có:
\(AB = BC.\cos B\), \(AC = BC.\sin B\).
b) + Trong tam giác AHB vuông tại H, ta có:
\(AH = AB.\sin B\); \(BH = AB.\cos B\).
+ \(CH = BC - BH\).
Advertisements (Quảng cáo)

(H.4.39)
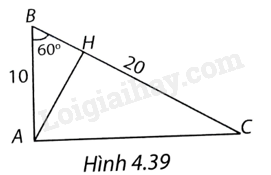
a) Trong tam giác ABC vuông tại A, ta có
\(AB = BC.\cos B = 20.\cos {60^o} = 10\),
\(AC = BC.\sin B = 20.\sin {60^o} = 10\sqrt 3 \).
b) Trong tam giác AHB vuông tại H, ta có
\(AH = AB.\sin B = 10.\sin {60^o} = 5\sqrt 3 \);
\(BH = AB.\cos B = 10.\cos {60^o} = 5\)
Do đó, \(CH = BC - BH = 20 - 5 = 15\left( {cm} \right)\)
