Chọn phương án đúng trong mỗi câu sau:
Câu 1
Trong Hình 4.35, \(\cos \alpha \) bằng
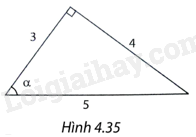
A. \(\frac{5}{3}\).
B. \(\frac{3}{4}\).
C. \(\frac{3}{5}\).
D. \(\frac{4}{5}\).

Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).

\(\cos \alpha = \frac{3}{5}\)
Chọn C
Câu 2
Trong tam giác MNP vuông tại M (H.4.36), \(\sin \widehat {MNP}\) bằng
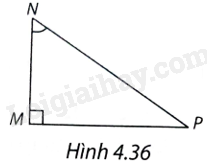
A. \(\frac{{PN}}{{NM}}\).
B. \(\frac{{MP}}{{PN}}\).
C. \(\frac{{MN}}{{PN}}\).
D. \(\frac{{MN}}{{MP}}\).

Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).

\(\sin \widehat {MNP} = \frac{{MP}}{{PN}}\)
Chọn B
Câu 3
Trong tam giác ABC vuông tại A (H.4.37), tanB bằng
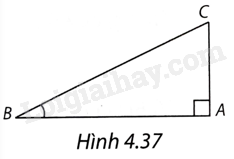
A. \(\frac{{AB}}{{AC}}\).
B. \(\frac{{AC}}{{AB}}\).
C. \(\frac{{AB}}{{BC}}\).
D. \(\frac{{BC}}{{AC}}\).

Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \).

Vì tam giác ABC vuông tại A nên \(tanB = \frac{{AC}}{{AB}}\)
Chọn B
Advertisements (Quảng cáo)
Câu 4
Với mọi góc nhọn \(\alpha \), ta có
A. \(\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \).
B. \(\tan \left( {{{90}^o} - \alpha } \right) = \cos \alpha \).
C. \(\cot \left( {{{90}^o} - \alpha } \right) = 1 - \tan \alpha \).
D. \(\cot \left( {{{90}^o} - \alpha } \right) = \sin \alpha \).

Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

\(\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \)
Chọn A
Câu 5
Giá trị \(\tan {30^o}\) bằng
A. \(\sqrt 3 \).
B. \(\frac{{\sqrt 3 }}{2}\).
C. \(\frac{1}{{\sqrt 3 }}\).
D. 1.

\(\tan {30^o} = \frac{1}{{\sqrt 3 }}\)

\(\tan {30^o} = \frac{1}{{\sqrt 3 }}\)
Chọn C
Câu 6
Cho tam giác MNP như Hình 4.38, MH là đường cao, \(\widehat {MPN} = {60^o},MN = 2\sqrt 3 \). Khi đó
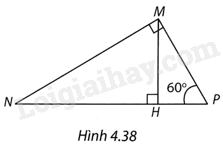
A. \(MP = \frac{1}{2}\).
B. \(\widehat {MNP} = {45^o}\).
C. \(MP = \frac{1}{3}\).
D. \(\widehat {MNP} = {30^o}\).

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc nhân với côtang góc kề.

Tam giác MNP vuông tại M nên
\(\widehat {MNP} = {90^o} - \widehat P = {30^o}\),
\(MP = MN.\cot {60^o} = 2\sqrt 3 .\frac{1}{{\sqrt 3 }} = 2\)
Chọn D
