
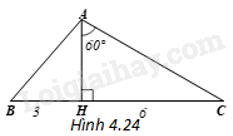
Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết \(HB = 3cm,HC = 6cm,\widehat {HAC} = {60^o}\). Hãy tính độ dài các cạnh (làm tròn đến cm), số đo các góc của tam giác ABC (làm tròn đến độ).

+ Tam giác vuông AHC có: \(\sin \widehat {HAC} = \frac{{HC}}{{AC}}\) nên tính được AC; \(AH = HC.\cot \widehat {HAC}\) nên tính được AH.
+ \(\widehat {ACB} = {90^o} - \widehat {HAC} = {30^o}\)
+ Áp dụng định lý Pythagore trong tam giác vuông AHB tính được AB.
+ \(\tan B = \frac{{AH}}{{BH}}\) từ đó tính được góc B.
+ Trong tam giác ABC, ta có: \(\widehat {BAC} = {180^o} - \widehat C - \widehat B\), từ đó tính được góc BAC.

(H.4.24)
Advertisements (Quảng cáo)
Tam giác ACH vuông tại H, \(HC = 6cm,\widehat {HAC} = {60^o}\).
Trong tam giác vuông AHC, ta có
\(\sin \widehat {HAC} = \frac{{HC}}{{AC}}\) nên
\(AC = \frac{{HC}}{{\sin \widehat {HAC}}} = \frac{6}{{\sin {{60}^o}}} = 4\sqrt 3 \approx 7\left( {cm} \right)\)
\(AH = HC.\cot \widehat {HAC} = 6.\cot {60^o} = 2\sqrt 3 \left( {cm} \right)\)
\(\widehat {ACB}\) là góc phụ với \(\widehat {HAC}\) nên \(\widehat {ACB} = {90^o} - \widehat {HAC} = {30^o}\)
Trong tam giác vuông AHB, ta có
\(A{B^2} = A{H^2} + H{B^2} = {3^2} + {\left( {2\sqrt 3 } \right)^2} = 21\) nên \(AB = \sqrt {21} \approx 5\left( {cm} \right)\)
\(\tan B = \frac{{AH}}{{BH}} = \frac{{2\sqrt 3 }}{3}\) nên \(\widehat B \approx {49^o}\)
Trong tam giác ABC, ta có
\(\widehat {BAC} = {180^o} - \widehat C - \widehat B = {180^o} - {30^o} - {49^o} \approx {101^o}\)
