Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \). Giải và trình bày phương pháp giải - Bài 3 trang 74 vở thực hành Toán 9 - Bài 11. Tỉ số lượng giác của góc nhọn. Cho tam giác vuông có một góc nhọn ({30^o}) và cạnh đối với góc này bằng 5cm...

Cho tam giác vuông có một góc nhọn \({30^o}\) và cạnh đối với góc này bằng 5cm. Tính độ dài cạnh huyền của tam giác

Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).

Advertisements (Quảng cáo)
(H.4.7)
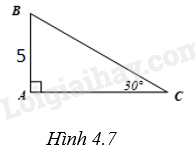
Xét tam giác ABC vuông tại A, có \(AB = 5\), \(\widehat C = {30^o}\). Ta cần tính cạnh BC.
Trong tam giác ABC vuông, ta có \(\sin C = \frac{{AB}}{{BC}}\), hay \(\sin {30^o} = \frac{{AB}}{{BC}}\), suy ra \(\frac{1}{2} = \frac{5}{{BC}}\), hay\(BC = 5:\frac{1}{2} = 10\left( {cm} \right)\)
