
Giải tam giác ABC vuông tại A, biết
a) \(BC = 20,\widehat C = {40^o}\);
b) \(AC = 82,\widehat B = {55^o}\);
c) \(BC = 32,AC = 20\).
(Kết quả về cạnh làm tròn đến chữ số thập phân thứ nhất, kết quả về góc làm tròn đến độ).

a) Ta có: \(\widehat B = {90^o} - \widehat C\); \(AC = BC.\cos C\); \(AB = BC.\sin C\).
b) Ta có: \(\widehat C = {90^o} - \widehat B\); \(AB = AC.\tan C\); \(B{C^2} = A{B^2} + A{C^2}\) nên tính được BC.
c) Ta có: \(A{B^2} = B{C^2} - A{B^2}\) tính được AB; \(\sin B = \frac{{AC}}{{BC}}\) tính được góc B; \(\widehat C = {90^o} - \widehat B\)

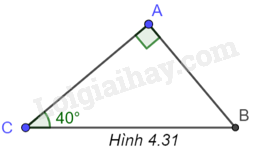
a) (H.4.31)
Advertisements (Quảng cáo)
Ta có: \(\widehat B = {90^o} - \widehat C = {50^o}\),
\(AC = BC.\cos C = 20.\cos {40^o} \approx 15,3\), \(AB = BC.\sin C = 20.\sin {40^o} \approx 12,9\)
b) (H.4.32)
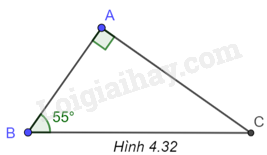
Ta có: \(\widehat C = {90^o} - \widehat B = {35^o}\).
\(AB = AC.\tan C = 82.\tan {35^o} \approx 57,4\)
\(B{C^2} = A{B^2} + A{C^2} = {82^2} + {57,4^2}\), suy ra \(BC = 100,1\)
c) (H.4.33)
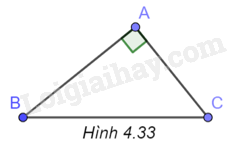
Ta có: \(A{B^2} = B{C^2} - A{B^2} = {32^2} - {20^2}\), suy ra \(AB \approx 25,0\)
\(\sin B = \frac{{AC}}{{BC}} = \frac{{20}}{{32}} = 0,625\), suy ra \(\widehat B \approx {39^o}\)
Từ đó suy ra \(\widehat C = {90^o} - \widehat B = {51^o}\)
