Cho tam giác \(ABC\) có trực tâm \(H\) và tâm đường tròn ngoại tiếp \(O\). Chứng minh rằng
a) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} \);
b) \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \).

(h.20).
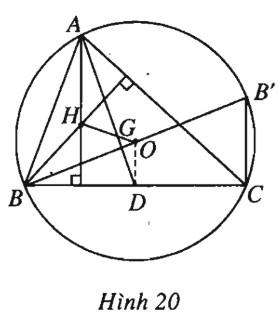
a) Gọi \(B’\) là điểm đối xứng với \(B\) qua \(O\), ta có \(B’C \bot BC\). Vì \(H\) là trực tâm tam giác \(ABC\) nên \(AH \bot BC\). Vậy \(AH//B’C.\)
Chứng minh tương tự ta có \(CH//B’A.\)
Vậy \(AB’CH\) là hình bình hành. Suy ra \(\overrightarrow {AH} = \overrightarrow {B’C} \). Gọi \(D\) là trung điểm của \(BC\) thì \(OD\) là đường trung bình của tam giác \(BB’C\) nên \(\overrightarrow {B’C} = 2\overrightarrow {OD} \). Vậy \(\overrightarrow {AH} = 2\overrightarrow {OD} \).
Từ đó, ta có
\(\overrightarrow {OA} = \overrightarrow {OH} + \overrightarrow {HA}\)
Advertisements (Quảng cáo)
\( = \overrightarrow {OH} - \overrightarrow {AH} = \overrightarrow {OH} - 2\overrightarrow {OD}\)
\( = \overrightarrow {OH} - (\overrightarrow {OB} + \overrightarrow {OC} ).\)
Suy ra \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} .\)
b) Gọi G là trọng tâm tam giác ABC thì
\(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 3\overrightarrow {HG}\)
\( = 3\overrightarrow {HO} + 3\overrightarrow {OG} \)
\(= 3\overrightarrow {HO} + \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} .\)
Kết hợp với kết quả của câu a), ta có
\(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 3\overrightarrow {HO} + \overrightarrow {OH} \)
\(= 2\overrightarrow {HO} .\)
