Advertisements (Quảng cáo)
Xét trong mặt phẳng tọa độ \(Oxy\). Biết \(M(x_1;y_1),\) \(N(x_2;y_2),\) \(P(x_3;y_3)\) là các trung điểm ba cạnh của một tam giác. Tìm tọa độ các đỉnh của tam giác.
(h.22).
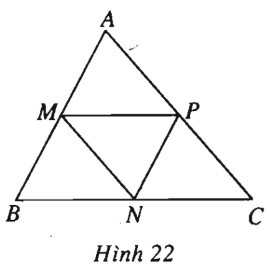
Giả sử tam giác ABC nhận \(M, N, P\) làm trung điểm của các cạnh \(AB, BC, CA\). Ta có
\(\,\,\,\overrightarrow {MA} = \overrightarrow {NP} \\ \Leftrightarrow \,\,\,\left\{ \matrix{ {x_A} – {x_M} = {x_P} – {x_N} \hfill \cr {y_A} – {y_M} = {y_P} – {y_N} \hfill \cr} \right.\\\Leftrightarrow \,\,\,\left\{ \matrix{ {x_A} = {x_1} – {x_2} + {x_3} \hfill \cr {y_A} = {y_1} – {y_2} + {y_3} \hfill \cr} \right.\)
Suy ra \(A = ({x_1} – {x_2} + {x_3}\,;\,{y_1} – {y_2} + {y_3}).\)
Tương tự ta tính được
\(B = ({x_1} + {x_2} – {x_3}\,;\,{y_1} + {y_2} – {y_3});\) \(C = ({x_2} + {x_3} – {x_1}\,;\,{y_2} + {y_3} – {y_1}).\)