Cho elip \((E)\) có phương trình \( \dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{4} = 1\).
a) Tìm tịa độ các tiêu điểm, các đỉnh; tính tâm sai và vẽ elip \((E)\).
b) Xác định m để đường thẳng \(d: y=x+m\) và \((E)\) có điểm chung.
c) Viết phương trình đường thẳng \(\Delta \) đi qua \(M(1 ; 1)\) và cắt \((E)\) tại hai điểm \(A, B\) sao cho \(M\) là trung điểm của đoạn thẳng \(AB\).

a) \({a^2} = 9 \Rightarrow a = 3 ,\) \( {b^2} = 4 \Rightarrow b = 2 ,\) \( {c^2} = {a^2} - {b^2} = 5 \Rightarrow c = \sqrt 5 \).
Các tiêu điểm : \({F_1}( - \sqrt 5 ; 0) ,{F_2}(\sqrt 5 ; 0) \).
Các đỉnh: \(( \pm 3 ; 0) , (0 ; \pm 2)\).
Tâm sai : \(e = \dfrac{{\sqrt 5 }}{3}\).
Elip được vẽ như hình 112.
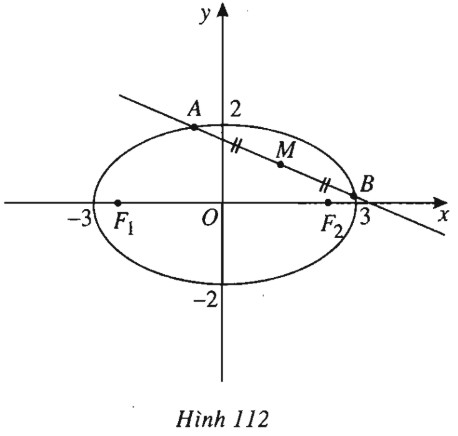
b) Hoành độ giao điểm của \(d\) và \((E)\) là nghiệm của phương trình:
\( \dfrac{{{x^2}}}{9} + \dfrac{{{{(x + m)}^2}}}{4} = 1\)
\( \Leftrightarrow 13{x^2} + 18mx + 9{m^2} - 36 = 0 \,\,\,\,\,\,\, (1)\)
Advertisements (Quảng cáo)
\(D\) và \((E)\) có điểm chung khi và chỉ khi (1) có nghiệm \( \Leftrightarrow \Delta ‘ \ge 0\)
\( \Leftrightarrow 81{m^2} - 13(9{m^2} - 36) \ge 0 \)
\( \Leftrightarrow {m^2} \le 13 \Leftrightarrow - \sqrt {13} \le m \le \sqrt {13} \).
Vậy với \( - \sqrt {13} \le m \le \sqrt {13} \) thì \(d\) và \((E)\) có điểm chung.
c) (h.112). Đường thẳng \(\Delta \) đi qua M, với vec tơ chỉ phương \(\overrightarrow u (a ; b)\) có dạng:
\(\left\{ \begin{array}{l}x = 1 + at\\y = 1 + bt\end{array} \right. \,\,\,\,\,({a^2} + {b^2} \ne 0)\)
\(A, B \in \Delta \Rightarrow \left\{ \begin{array}{l}{x_A} = 1 + a{t_1}\\{y_A} = 1 + b{t_1}\end{array} \right.\) và \(\left\{ \begin{array}{l}{x_B} = 1 + a{t_2}\\{y_B} = 1 + b{t_2}\end{array} \right.\).
\(M\) là trung điểm của \(AB\) khi và chỉ khi \(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_M}\\{y_A} + {y_B} = 2{y_M}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a({t_1} + {t_2}) = 0\\b({t_1} + {t_2}) = 0\end{array} \right.\)
\( \Leftrightarrow {t_1} + {t_2} = 0 (1) \) (do \({a^2} + {b^2} \ne 0\)).
\(A, B \in (E)\) suy ra \({t_1}, {t_2}\) là nghiệm của phương trình:
\(\begin{array}{l}4{(at + 1)^2} + 9{(bt + 1)^2} = 36 \\ \Leftrightarrow (4 {a^2} + 9{b^2}){t^2} + (8a + 18b)t - 23 = 0.\\{t_1} + {t_2} = 0 \\ \Rightarrow 8a + 18b = 0 \\ \Leftrightarrow 4a + 9b = 0.\end{array}\)
Chọn \(a=9, b=-4,\) ta được phương trình của \(\Delta : \left\{ \begin{array}{l}x = 1 + 9t\\y = 1 - 4t\end{array} \right.\) hay \(4x + 9y - 13 = 0\).
