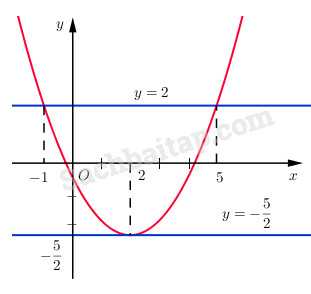
Tìm hàm số bậc hai có đồ thị là parabol \((P)\), biết rằng đường thẳng \(y = -2,5\) có một điểm chung duy nhất với \((P)\) và đường thẳng \(y = 2\) cắt \((P)\) tại hai điểm có hoành độ là -1 và 5. Vẽ parabol \((P)\) cùng các đường thẳng \(y = -2,5\) và \(y = 2\) trên cùng một mặt phẳng tọa độ.

Đường thẳng \(y = -2,5\) song song với trục hoành. Do đường thẳng này có một điểm chung duy nhất với parabol \((P)\) nên điểm chung ấy chính là đỉnh của parabol \((P)\). Từ đó suy ra đỉnh \((I)\) của parabol \((P)\) có tung độ \(y = -2,5.\)
Đường thẳng \(y = 2\) cũng song song với trục hoành. Do đó trung điểm \(C\) của đoạn thẳng \(AB\) nằm trên trục đối xứng của parabol.
Hoành độ của điểm \(C\) là \(x = {{ - 1 + 5} \over 2} = 2.\)
Vậy trục đối xứng của parabol là đường thẳng \(x = 2\), suy ra hoành độ đỉnh \(I\) của \((P)\) là \(x = 2.\)
Advertisements (Quảng cáo)
Tọa độ của \(I\) là \((2 ; -2,5)\). Từ đó suy ra nếu \((P)\) là đồ thị của hàm số \(f(x) = a{x^2} + bx + c\) thì
\(f\left( { - 1} \right) = a - b + c = 2, - {b \over {2a}} = 2\) và \( - {\Delta \over {4a}} = - {{{b^2} - 4ac} \over {4a}} = - 2,5.\)
Từ đó suy ra \(a = {1 \over 2},b = - 2,c = - {1 \over 2}\) và hàm số cần tìm là \(y = {1 \over 2}{x^2} - 2x - {1 \over 2}.\)
Đồ thị của hàm số