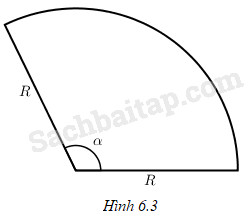
Xét hình quạt tròn bán kính R, góc ở tâm \(\alpha \left( {R > 0,0 < \alpha < 2\pi } \right)\)(h.6.3).
a) Biết diện tích hình tròn bán kính R là \(\pi {R^2}\) và diện tích hình quạt tròn tỉ lệ thuận với số đo góc ở tâm. Hãy tính diện tích hình quạt tròn nói trên. Hỏi \(\alpha \) bằng bao nhiêu thì diện tích đó bằng \({R^2}\) ?
b) Gọi chu vi hình quạt tròn là tổng độ dài hai bán kính và độ dài cung tròn của hình quạt đó. Trong các hình quạt có chu vi cho trước, tìm hình quạt có diện tích lớn nhất.
c) Trong các hình quạt có diện tích cho trước, tìm hình quạt có chu vi nhỏ nhất.

Advertisements (Quảng cáo)
a) Diện tích hình quạt tròn với bán kính R và góc ở tâm \(\alpha \) là
\(S = \dfrac{{\pi {R^2}}}{{2\pi }}\alpha = \dfrac{1}{2}{R^2}\alpha \). Từ đó \(S = {R^2} \Leftrightarrow \alpha = 2\).
b) Chu vi hình quạt tròn nói trên là \(C = 2R + R\alpha \). Hai số dương 2R và \(R\alpha \) có tổng không đổi nên tích \(2R.R\alpha = 4S\) đạt giá trị lớn nhất khi và chỉ khi \(2R = R\alpha \Leftrightarrow \alpha = 2\).
c) Hai số dương 2R và \(R\alpha \) có tích \(2R.R\alpha = 4S\)không đổi, nên tổng \(2R + R\alpha = C\) đạt giá trị nhỏ nhất khi và chỉ khi \(2R = R\alpha \Leftrightarrow \alpha = 2\).
