Cho tam giác ABC. Chứng minh rằng nếu \(\left| {\overrightarrow {CA} - \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA} - \overrightarrow {CB} } \right|\) thì tam giác ACB là tam giác vuông cân tại C.
Gợi ý làm bài
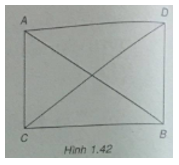
Vẽ hình bình hành CADB.
Ta có \(\overrightarrow {CA} + \overrightarrow {CB} = \overrightarrow {CD} \), do đó \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = CD\)
Advertisements (Quảng cáo)
Vì \(\overrightarrow {CA} - \overrightarrow {CB} = \overrightarrow {BA} \), do đó \(\left| {\overrightarrow {CA} - \overrightarrow {CB} } \right| = BA\)
Từ \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA} - \overrightarrow {CB} } \right|\) suy ra CD = AB (h.1.42)
Vậy tứ giác CADB là hình chữ nhật. Ta có tam giác ACB vuông tại C.