Cho tứ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Bài 1.3 trang 12 Sách bài tập (SBT) Toán Hình học 10 - Bài 1: Các định nghĩa
Cho tứ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh \(\overrightarrow {NP} = \overrightarrow {MQ} \) và \(\overrightarrow {PQ} = \overrightarrow {NM} \)
Gợi ý làm bài
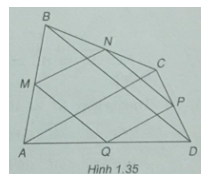
(h. 1.35)
Advertisements (Quảng cáo)
MN = PQ và MN // PQ
Vì chúng đều bằng \({1 \over 2}\) AC và đều song song với AC .
Vậy tứ giác MNPQ là hình bình hành nên ta có:
\(\overrightarrow {NP} = \overrightarrow {MQ} ,\overrightarrow {PQ} = \overrightarrow {NM} \)
