Cho tứ giác ABCD.. Bài 1.32 trang 34 Sách bài tập (SBT) Toán Hình học 10 - Bài 3: Tích của vec tơ với một số
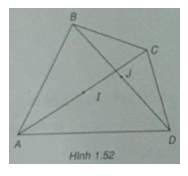
Cho tứ giác ABCD. Gọi I và J lần lượt là trung điểm của hai đường chéo AC và BD. Chứng minh \(\overrightarrow {AB} + \overrightarrow {CD} = 2\overrightarrow {IJ} \)
Gợi ý làm bài
(h.1.52)
Advertisements (Quảng cáo)
\(\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AB} + \overrightarrow {BJ}\)
\(\overrightarrow {IJ} = \overrightarrow {IC} + \overrightarrow {CD} + \overrightarrow {DJ} \)
Cộng từng vế hai đẳng thức trên ta được
\(\eqalign{
& 2\overrightarrow {IJ} = (\overrightarrow {IA} + \overrightarrow {IC} ) + \overrightarrow {AB} + \overrightarrow {CD} + (\overrightarrow {BJ} + \overrightarrow {DJ} ) \cr
& = \overrightarrow {AB} + \overrightarrow {CD} \cr} \)