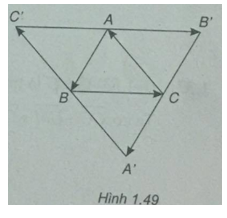
Cho tam giác ABC. Dựng \(\overrightarrow {A’B} = \overrightarrow {BC} ,\overrightarrow {C’A} = \overrightarrow {AB} \) và \(\overrightarrow {BC’} = \overrightarrow {CA} \)
a) Chứng minh rằng A là trung điểm của B’C’
b) Chứng minh các đường thẳng AA’, BB’, CC’ đồng quy
Gợi ý làm bài
Advertisements (Quảng cáo)
a) \(\overrightarrow {BC’} = \overrightarrow {CA} \) => Tứ giác ACBC’ là hình bình hành => \(\overrightarrow {AC’} = \overrightarrow {CB} \)
\(\overrightarrow {AB’} + \overrightarrow {AC’} = \overrightarrow {BC} + \overrightarrow {CB} = \overrightarrow {BB} = \overrightarrow 0 \) =>A là trung điểm của B’C’
b) Vì tứ giác ACBC’ là hình bình hành nên CC’ chứa trung tuyến của tam giác ABC xuất phát từ đỉnh C. Tương tự như vậy với AA’, BB’. Do đó AA’, BB’, CC’ đồng quy tại trọng tâm G của tam giác ABC.