Cho hai hình bình hành ABCD và ABEF với A, D, F không thẳng hàng. Dựng các vec tơ $\(\overrightarrow {EH} \) và \(\overrightarrow {FG} \) bằng vec tơ \(\overrightarrow {AD} \). Chứng minh tứ giác CDGH là hình bình hành.
Gợi ý làm bài
(h.1.64)
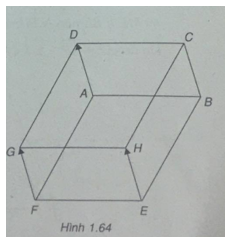
\(\overrightarrow {EH} = \overrightarrow {AD} ,\overrightarrow {FG} = \overrightarrow {AD} = > \overrightarrow {EH} = \overrightarrow {FG} \)
=>Tứ giác FEHG là hình bình hành
Advertisements (Quảng cáo)
\( = > \overrightarrow {GH} = \overrightarrow {FE} \,(1)\)
Ta có: \(\overrightarrow {DC} = \overrightarrow {AB} ,\overrightarrow {AB} = \overrightarrow {FE} \)
\(\overrightarrow { = > DC} = \overrightarrow {FE} \,(2)\)
Từ (1) và (2) ta có \(\overrightarrow {GH} = \overrightarrow {DC} \)
Vậy tứ giác GHCD là hình bình hành.
