Cho lục giác đều ABCDEF và M là một điểm tùy ý. Chứng minh rằng. Bài 1.52 trang 45 Sách bài tập (SBT) Toán Hình học 10 - Ôn tập chương I
Cho lục giác đều ABCDEF và M là một điểm tùy ý. Chứng minh rằng:
\(\overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {ME} = \overrightarrow {MB} + \overrightarrow {MD} + \overrightarrow {MF} \)
Gợi ý làm bài
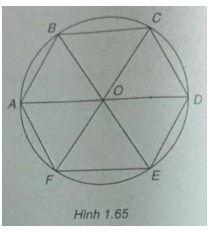
(h.1.65)
Advertisements (Quảng cáo)
Gọi O là tâm lục giác đều. Khi đó O là trọng tâm của các tam giác đều ACE và BDF.
Do đó, với mọi điểm M ta có:
\(\overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {ME} = 3\overrightarrow {MO} \)
\(\overrightarrow {MB} + \overrightarrow {MD} + \overrightarrow {MF} = 3\overrightarrow {MO} \)
Vậy ta có đẳng thức cần chứng minh.
