Cho hình bình hành ABCD. Dựng \(\overrightarrow {AM} = \overrightarrow {BA} \), \(\overrightarrow {MN} = \overrightarrow {DA} \), \(\overrightarrow {NP} = \overrightarrow {DC} \), \(\overrightarrow {PQ} = \overrightarrow {BC} \). Chứng minh \(\overrightarrow {AQ} = \overrightarrow 0 \)
Gợi ý làm bài
(h.1.40)
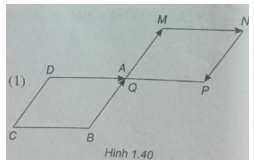
\(\overrightarrow {AM} = \overrightarrow {BA} \)
\(\overrightarrow {NP} = \overrightarrow {DC} = \overrightarrow {AB} \)
Advertisements (Quảng cáo)
Suy ra AM = NP và AM // NP. Vậy tứ giác AMNP là hình bình hành. (1)
Ta có \(\overrightarrow {PQ} = \overrightarrow {BC} \)
\(\overrightarrow {MN} = \overrightarrow {DA} = \overrightarrow {CB} \)
Suy ra PQ = MN và P Q // MN . Vậy tứ giác MNPQ là hình bình hành (2).
Từ (1) và (2) suy ra A = Q hay \(\overrightarrow {AQ} = \overrightarrow 0 \)
