Cho tam giác ABC. Gọi H là trực tâm của tam giác và M là trung điểm của cạnh BC. Chứng minh rằng \(\overrightarrow {MH} .\overrightarrow {MA} = {1 \over 4}B{C^2}\)
Gợi ý làm bài
(h.2.24)
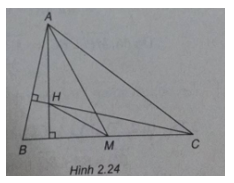
Ta có \(\overrightarrow {AM} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {AC} )\)
\(\overrightarrow {HM} = {1 \over 2}(\overrightarrow {HB} + \overrightarrow {HC} )\)
\( = > \overrightarrow {AM} .\overrightarrow {HM} = {1 \over 4}(\overrightarrow {AB} + \overrightarrow {AC} ).(\overrightarrow {HB} + \overrightarrow {HC} )\)
Advertisements (Quảng cáo)
\( = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {HB} + \underbrace {\overrightarrow {AB} .\overrightarrow {HC} }_{ = 0} + \underbrace {\overrightarrow {AC} \overrightarrow {.HB} }_{ = 0} + \overrightarrow {AC} .\overrightarrow {HC} )\)
\( = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {HB} + \overrightarrow {AC} .\overrightarrow {HC} )\)
\( = {1 \over 4}\left[ {\overrightarrow {AB} .(\overrightarrow {HC} + \overrightarrow {CB} ) + \overrightarrow {AC} .(\overrightarrow {HB} + \overrightarrow {BC} )} \right]\)
\( = {1 \over 4}\left[ {\underbrace {\overrightarrow {AB} .\overrightarrow {HC} }_0 + \overrightarrow {AB} .\overrightarrow {CB} + \underbrace {\overrightarrow {AC} .\overrightarrow {HB} }_0 + \overrightarrow {AC} .\overrightarrow {BC} } \right]\)
\( = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {CB} + \overrightarrow {AC} .\overrightarrow {BC} ) = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {CB} - \overrightarrow {AC} .\overrightarrow {CB} )\)
\( = {1 \over 4}\overrightarrow {CB} .(\underbrace {\overrightarrow {AB} - \overrightarrow {AC} }_{\overrightarrow {CB} }) = {1 \over 4}{\overrightarrow {CB} ^2} = {1 \over 4}{\overrightarrow {BC} ^2}\)
