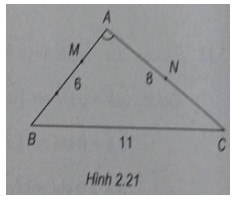
Tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 11 cm.
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \) và chứng tỏ rằng tam giác ABC có góc A tù.
b) Trên cạnh AB lấy điểm M sao cho AM = 2 cm và gọi N là trung điểm của cạnh AC. Tính \(\overrightarrow {AM} .\overrightarrow {AN} \).
Gợi ý làm bài
(h.2.21)
a)
Advertisements (Quảng cáo)
\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {AC} = {1 \over 2}(A{C^2} + A{B^2} - B{C^2}) \cr
& = {1 \over 2}({8^2} + {6^2} - {11^2}) = - {{21} \over 2} \cr} \)
\( = AB.AC.cosA = - {{21} \over 2}\)
=> Góc A tù
b) Ta có:
\(\overrightarrow {AM} = {1 \over 3}\overrightarrow {AB} ,\overrightarrow {AN} = {1 \over 2}\overrightarrow {AC} \)
Do đó:
\(\eqalign{
& \overrightarrow {AM.} \overrightarrow {AN} = {1 \over 3}\overrightarrow {AB} .{1 \over 2}\overrightarrow {AC} \cr
& = {1 \over 6}\overrightarrow {AB} .\overrightarrow {AC} = {1 \over 6}.( - {{21} \over 2}) = - {7 \over 4} \cr}\)
