Chứng minh rằng diện tích hình bình hành bằng tích hai cạnh liên tiếp với sin của góc xen giữa chúng.
Gợi ý làm bài
(h.2.29)
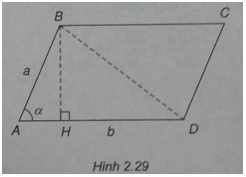
Xét hình bình hành ABCD có \(AB = a,AD = b,\widehat {BAD} = \alpha \) và BH là đường cao, ta có \(BH \bot AD\) tại H
Gọi S là diện tích hình bình hành ABCD, ta có S = AD. BH với \(BH = AB\sin \alpha \)
Advertisements (Quảng cáo)
Vậy \(S = AD.AB\sin \alpha = a.b.\sin \alpha \)
Nếu \(\widehat {BAD} = \alpha \) thì \(\widehat {ABC} = {180^0} - \alpha \)
Khi đó ta vẫn có \(\sin \widehat {BAD} = \sin \widehat {ABC}\)
Khi đó ta vẫn có
Nhận xét: Diện tích hình bình hành ABCD gấp đôi diện tích tam giác ABD mà tam giác ABD có diện tích là \({1 \over 2}ab\sin \alpha \). Do đó ta suy ra diện tích của hình bình hành bằng \(ab\sin \alpha \)
