Giả sử chúng ta cần đo chiều cao CD của một cái tháp với C là chân tháp, D là đỉnh tháp. Vì không thể đến chân tháp được nên từ hai điểm A, B có khoảng cách AB = 30 m sao cho ba điểm A, B, C thẳng hàng người ta đo được các góc \(\widehat {CAD} = {43^0},\widehat {CBD} = {67^0}\) (h.2.18). Hãy tính chiều cao CD của tháp
Gợi ý làm bài
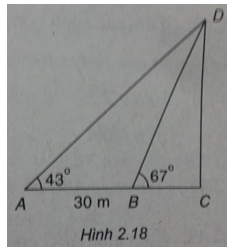
Muốn tính chiều cao CD của tháp, trước hết ta hãy tính góc \(\widehat {ADB}\)
\(\widehat {ADB} = {67^0} - {43^0} = {24^0}\)
Theo định lí sin đối với tam giác ABD ta có:
Advertisements (Quảng cáo)
\(\eqalign{
& {{BD} \over {\sin {{43}^0}}} = {{AB} \over {\sin {{24}^0}}} \cr
& = > BD = {{30.\sin {{43}^0}} \over {\sin {{24}^0}}} \approx 50,30(m) \cr} \)
Trong tam giác vuông BCD ta có:
\(\eqalign{
& \sin {67^0} = {{CD} \over {BD}} \cr
& = > CD = BD.\sin {67^0} \approx 50,30.\sin {67^0} \cr} \)
Hay \(CD \approx 46,30(m)\)
Sachbaita.net
