Trong mặt phẳng tọa độ Oxy cho hình chữ nhật ABCD có điểm I(6;2) là giao điểm của hai đường chéo AC và BD. Điểm M(1;5) thuộc đường thẳng AB và trung điểm E của cạnh CD thuộc đường thẳng \(\Delta 😡 + y - 5 = 0\). \(\Delta 😡 + y - 5 = 0\)
Gợi ý làm bài
(Xem hình 3.14)
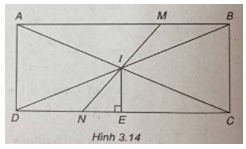
Gọi N là điểm đối xứng với M qua I, suy ra N(11 ; -1) và điểm N thuộc đường thẳng CD.
\(E \in \Delta \Rightarrow E(x;5 - x)\,;\,\overrightarrow {IE} = (x - 6;3 - x)\)
và: \(\overrightarrow {NE} = (x - 11;6 - x)\)
E là trung điểm của CD \( \Rightarrow IE \bot EN.\)
Advertisements (Quảng cáo)
\(\overrightarrow {IE} .\overrightarrow {NE} = 0 \Leftrightarrow \left( {x - 6} \right)\left( {x - 11} \right) + \left( {3 - x} \right)\left( {6 - x} \right) = 0\)
\(\overrightarrow {IE} .\overrightarrow {NE} = 0 \Leftrightarrow \left( {x - 6} \right)\left( {x - 11} \right) + \left( {3 - x} \right)\left( {6 - x} \right) = 0\)
\( \Leftrightarrow x = 6\) hoặc x = 7
Với \(x = 6 \Rightarrow \overrightarrow {IE} = (0;3),\)
Phương trình \(AB:y - 5 = 0.\)
Với \(x = 7 \Rightarrow IE = \left( {1; - 4} \right),\)
Phương trình \(AB:x - 4y + 19 = 0.\)
