Trong mặt phẳng tọa độ Oxy, hãy xác định tọa độ đỉnh C của tam giác ABC biết rằng hình chiếu vuông góc của C trên đường thẳng AB là điểm H(-1;-1), đường phân giác trong của góc A có phương trình x - y + 2 = 0 và đường cao kẻ từ B có phương trình 4x + 3y - 1 = 0
Gợi ý làm bài
Ta gọi \({d_1}:x - y + 2 = 0\) và \({d_2}:4x + 3y - 1 = 0\).
Gọi H'(a;b) là điểm đối xứng của H qua \({d_1}\)
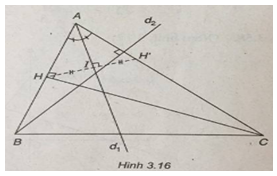
Khi đó H’ thuộc đường thẳng AC (h.3.16).
\(\overrightarrow u = (1;1)\) là vectơ chỉ phương của \({d_1}\), \(\overrightarrow {HH’} = \left( {a + 1;b + 1} \right)\) vuông góc với \(\overrightarrow u \) và trung điểm \(I\left( {{{a - 1} \over 2};{{b - 1} \over 2}} \right)\) của \(\overrightarrow {HH’} \) thuộc \({d_1}\). Do đó tọa độ của H’ là nghiệm của hệ phương trình:
\(\left\{ \matrix{
1.\left( {a + 1} \right) + 1\left( {b + 1} \right) = 0 \hfill \cr
{{a - 1} \over 2} - {{b - 1} \over 2} = 0 \hfill \cr} \right. \Rightarrow H'( - 3;1).\)
Advertisements (Quảng cáo)
Đường thẳng AC đi qua H’ vuông góc với \({d_2}\) nên có viectơ pháp tuyến là \(\overrightarrow v = \left( {3; - 4} \right)\), suy ra AC có phương trình là :
\(\eqalign{
& 3\left( {x + 3} \right) - 4\left( {y - 1} \right) = 0 \cr
& \Leftrightarrow 3x - 4y + 13 = 0. \cr} \)
Tọa độ của A là nghiệm của hệ phương trình \(\left\{ \matrix{
3x - 4y + 13 = 0 \hfill \cr
x - y + 2 = 0 \hfill \cr} \right.\)
\( \Rightarrow A(5;7).\)
Đường thẳng CH đi qua H (-1 ; -1) với vectơ pháp tuyến là \({1 \over 2}\overrightarrow {HA} = \left( {3;4} \right)\) nên có phương trình là:
\(3\left( {x + 1} \right) + 4\left( {y + 1} \right) = 0 \Leftrightarrow 3x + 4y + 7 = 0.\)
Tọa độ của C là nghiệm của phương trình
\(\left\{ \matrix{
3x + 4y + 7 = 0 \hfill \cr
3x - 4y + 13 = 0 \hfill \cr} \right. \Rightarrow C\left( { - {{10} \over 3};{3 \over 4}} \right).\)
