Trong mặt phẳng tọa độ Oxy, tìm điểm A thuộc trục hoành và điểm B thuộc trục tung sao cho A và B đối xứng với nhau qua đường thẳng d: x - 2y + 3 = 0.
Gợi ý làm bài
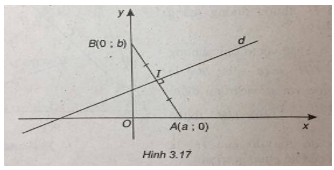
(Xem hình 3.17)
\(\eqalign{
& A \in Ox\,\,B \in Oy \cr
& \Rightarrow A\left( {a;0} \right),B\left( {0;b} \right),AB = \left( { - a;b} \right). \cr} \)
Advertisements (Quảng cáo)
Vectơ chỉ phương của d là \(\overrightarrow u = \left( {2;1} \right)\)
Tọa độ trung điểm I của AB là \(\left( {{a \over 2};{b \over 2}} \right)\).
A và B đối xứng với nhau qua d khi và chỉ khi:
\(\left\{ \matrix{
\overrightarrow {AB} .\overrightarrow u = 0 \hfill \cr
I \in d \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
- 2a + b = 0 \hfill \cr
{a \over 2} - b + 3 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 2 \hfill \cr
b = 4. \hfill \cr} \right.\)
Vậy \(A\left( {2;0} \right),B\left( {0;4} \right).\)
