Trong mặt phẳng tọa độ Oxy, cho điểm A( 2;2) và các đường thẳng
\({d_1}:x + y - 2 = 0\); \({d_2}:x + y - 8 = 0\)
Tìm tọa độ các điểm B và C lần lượt thuộc \({d_1}\) và \({d_2}\) sao cho tam giác ABC vuông cân tại A.
Gợi ý làm bài
(xem hình 3.19)
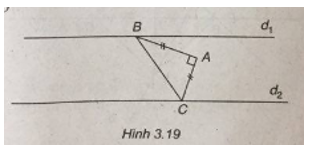
Vì \(B \in {d_1},C \in {d_2}\) nên \(B\left( {b;2 - b} \right),C\left( {c;8 - c} \right).\)
Advertisements (Quảng cáo)
Tam giác ABC vuông cân tại A
\(\eqalign{
& \Leftrightarrow \left\{ \matrix{
\overrightarrow {AB} .\overrightarrow {AC} = 0 \hfill \cr
AB = AC \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
bc - 4b - c + 2 = 0 \hfill \cr
{b^2} - 2b = {c^2} - 8c + 18 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
(b - 1)(c - 4) = 2 \hfill \cr
{(b - 1)^2}{(c - 4)^2} = 3. \hfill \cr} \right. \cr} \)
Đặt x = b – 1, y = c – 4 ta có hệ :
\(\left\{ \matrix{
x.y = 2 \hfill \cr
{x^2} - {y^2} = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 2 \hfill \cr
y = - 1 \hfill \cr} \right.\)
hoặc
\(\left\{ \matrix{
x = 2 \hfill \cr
y = 1. \hfill \cr} \right.\)
Vậy B(-1 ; 3), C(3 ; 5) hoặc B(3 ; -1), C(5;3)
