Một máy bay bay với vận tốc không đổi \({v_0}\) theo phương nằm ngang ở độ cao h so với mặt đất và thả một vật.
a. Nếu h = 2,5km; \({v_0}\) = 120 m/s. hãy :
+ Lập phương trình quỹ đạo của vật.
+ Xác định thời gian từ lúc thả vật đến lúc vật chạm đất. Tìm quãng đường \(l\) vật đi được theo phương nằm ngang kể từ lúc được thả cho tới khi chạm đất.
b. Khi h=1000m, hãy tính \({v_0}\) để l =1500m.
Bỏ qua ảnh hưởng của không khí.

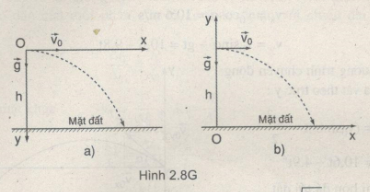
a.+) Nếu chọn hệ trục tọa độ như hình 2.8G ( gốc tọa độ ở điểm thả vật, Ox hướng theo \({\vec v_0}\), Oy hướng thẳng đướng xuống dưới) thì:
\({a_x} = 0\) ; \(x = {v_0}t = 120t\)
\({a_y} = g\);\(y = {{g{t^2}} \over 2} = 4,9{t^2}\)
Rút t từ biểu thức của x thay vào biểu thức của y ta được:
\(y = {{4,9} \over {{{120}^2}}}{x^2}\)
Advertisements (Quảng cáo)
Nếu chọn hệ trục như hình 2.8G b ( gốc tọa độ là hình chiếu của điểm thả vật trên mặt đất, Ox song song với \({\vec v_0}\). Oy hướng thẳng đứng lên trên) thì :
\({a_x} = 0;\) \(x = {v_0}t = 120t\)
\({a_y} = - g\) ; \(y = {y_0} - {{g{t^2}} \over 2} = 2500 - 4,9{t^2}\)
Từ đó \(y = 2500 - {{4,9} \over {{{120}^2}}}{x^2}\)
+) Thời gian từ lúc thả vật đến lúc vật chạm đất là : \(t = \sqrt {{{2h} \over g}} \approx 22,6s\)
Từ đó : \(l = {v_0}t = 120.22,6 = 2712m.\)
b. \({v_0} = {l \over t} = l\sqrt {{g \over {2h}}} \approx 105m/s\)
