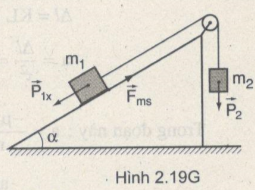
Trong hệ ở Hình 2.18,ta có :
\({m_1} = 500g;\alpha = {30^0};\)
các hệ số ma sát trượt và ma sát nghỉ giữa vật 1 và mặt phẳng nghiêng là \({\mu _t} = {\mu _n} = 0,2.\) Mặt phẳng nghiêng được giữ cố định. Hãy tính gia tốc của mỗi vật m1, m2 và lực ma sát giữa vật 1 với mặt phẳng nghiêng trong các trường hợp :
a)m1=500g;
b)m2=200g.
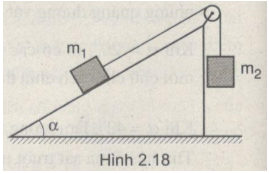

a)Nhận xét : \({P_2} > {P_{1x}} + {F_{msn\max }}\) nên vật m1 chuyển động lên trên, vật m2 chuyểnđộng xuống dưới (Hình 2.18G). Gia tốc của hệ bằng :
\(\eqalign{ & a = {{{P_2} - {P_{1x}} - {F_{mst}}} \over {{m_1} + {m_2}}} \cr & = {{{m_2}g - {m_1}g\sin \alpha - {m_1}{\mu _t}g\cos \alpha } \over {{m_1} + {m_2}}} \cr & = 1,6m/{s^2} \cr} \)
Trong đó ta đã thay \({F_{msn\max }} = {F_{mst}},\) bằng :
Advertisements (Quảng cáo)
\({F_{mst}} = {\mu _t}{m_1}g\cos \alpha \approx 0,85N\)
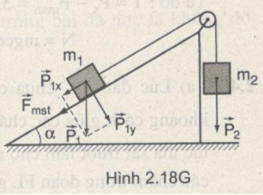
b)Trong trường hợp này ta nhận thấy :
\({P_{1x}} < {P_2} + {F_{msn\max }}(1)\)
Nên hệ không chuyển động (Hình 2.19G)
Ta có a =0.
Lúc này lực ma sát nghỉ chưa đạt tới giá trị cực đại :
\({F_{msn}} = {P_{1x}} - {P_2} = g({m_1}\sin \alpha - {m_2}) = 0,49N\)