Người ta bố trí một cơ hệ như ở Hình 2.21a. Vật m2 có gắn một băng giấy luồn qua bộ rung đo thời gian.
Khi thả cho hệ chuyển động, bộ rung lần lượt ghi lại trên băng giấy những chấm đen sau từng khoảng thời gian \(t = 0,04s\) như Hình 2.21b.
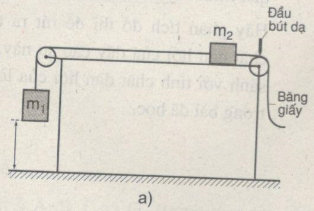

Ta đo được :
|
Đoạn thẳng |
AB |
BC |
CD |
DE |
EF |
FG |
GH |
HI |
IK |
KL |
|
Chiều dài (mm) |
17 |
28 |
39 |
50 |
Advertisements (Quảng cáo) 61 |
59 |
54 |
49 |
44 |
39 |
a) Giải thích sự biến thiên của chiều dài các đoạn trên.
b) Dựa vào các chấm từ G đến L để xác định hệ số ma sát trượt giữa bàn và vật 2.
c) Dựa vào các chấm từ A đến E để xác định m2, nếu biết m1 =400g.

a)Lúc đầu ( m1 chưa chạm đất ), hệ chuyển động nhanh dần đều, nên khoảng cách giữa các chấm trong đoạn AF tăng dần.Sau khi m1chạm đất,lực ma sát trượt làm cho m2 chuyển động chậm dần, nên khoảng cách giữa các chấm trong đoạn FL giảm dần.
b)Trong đoạn GL:
\(\eqalign{ & \Delta l = KL - IK = IK - HI = HI - GH = - 5mm \cr & a = {{\Delta l} \over {{t^2}}} = {{ - {{5.10}^{ - 3}}} \over {0,{{04}^2}}} \approx - 3,125m/{s^2} \cr} \)
Trong đoạn này : \(a = {{ - {\mu _t}{m_2}g} \over {{m_2}}} = - {\mu _t}g\)
\({\mu _t} = - {a \over g} = 0,32\)
c)Trong đoạn AE :
\(\eqalign{ & \Delta l’ = DE - CD = CD - BC = BC - AB = 11mm \cr & a’ = {{\Delta l’} \over {{t^2}}} = {{{{11.10}^{ - 3}}} \over {0,{{04}^2}}} \approx 6,88m/{s^2} \cr} \)
Trong đoạn này : \(a’ = {{\left( {{m_1} - {\mu _t}{m_2}} \right)g} \over {{m_1} + {m_2}}}\)
Rút ra : \({m_2} = {{{m_1}\left( {g - a’} \right)} \over {a’ + {\mu _t}g}} = 0,117kg.\)
