Từ một đỉnh tháp cao 12 m so với mặt đất, người ta ném một hòn đá với vận tốc ban đầu v0 = 15 m/s, theo phương hợp với phương nằm ngang một góc \(\alpha = {45^0}\). Xác định phương, chiều, độ lớn của vận tốc hòn đá khi nó chạm đất. Bỏ qua lực cản của không khí.

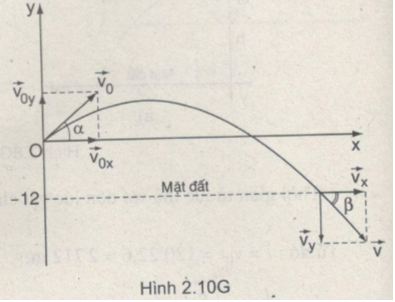
Chọn hệ trục tọa độ như Hình 2.10G ( gốc tọa độ là đỉnh tháp ). Phương trình vận tốc của vật :
\(\eqalign{ & {v_x} = {v_0}\cos \alpha = 10,6m/s(1) \cr & {v_y} = {v_0}\sin \alpha - gt = 10,6 - 9,8t(2) \cr} \)
Phương trình chuyển động của vật theo trục y :
\(\eqalign{ & y = ({v_0}\sin \alpha )t - {{g{t^2}} \over 2} \cr & = 10,6t - 4,9{t^2} \cr} \)
Khi hòn đá tới đất :
y = -12 m. Ta có :
Advertisements (Quảng cáo)
\( = 10,6t - 4,9{t^2} = - 12.\)
Phương trình này có một nghiệm dương: t = 2,98 s.
Thay vào (2), ta có :
\({v_y} = - 18,6m/s\)
Độ lớn của vận tốc khi vật chạm đất :
\(v = \sqrt {v_x^2 + v_y^2} = \sqrt {10,{6^2} + 18,{6^2}} \)\(\,= 21,4m/s\)
Vận tốc này hợp với phương nằm ngang một góc \(\beta :\)
\(\cos \beta = {{{v_x}} \over v} \approx 0,5\) hay \(\beta \approx {60^ \circ }\)
