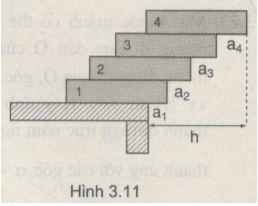
Bốn viên gạch giống hệt nhau, có chiều dài L, được đặt chồng lên nhau sao cho mỗi phần của mỗi viên nhô ra ngoài viên nằm dưới (Hình 3.11).
Hãy tính :
a) Các giá trị lớn nhất của các đoạn \({a_1},{a_2},{a_3},{a_4}\) nhô ra của mỗi viên sao cho chồng gạch vẫn cân bằng.
b) Khoảng cách h từ mép bán đến mép ngoài cùng một viên gạch trên cùng nhô ra.
Advertisements (Quảng cáo)

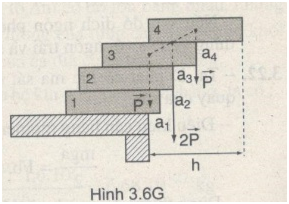
a) Xét viên gạch 4 nằm trên cùng. Nó chỉ có thể nhô ra ngoài viên gạch 3 nhiều nhất bằng nửa chiều dài L của gạch : \({a_4} = {1 \over 2}L.\) Tiếp theo, để hệ hai viên gạch 3 và 4 nằm cân bằng thì giới hạn ngoài cùng của đường tác dụng của trọng lực hệ hai viên gạch 3 và 4 là mép phải của viên gạch 2. Vị trí của đường đó được xác định bằng quy tắc tổng hợp hai lực song song , cùng chiều ( bằng nhau, bằng trọng lượng của mỗi viên). Đường này nằm cách mép phải của viên gạch 2 một đoạn \({a_3} = {1 \over 4}L.\) Tương tự, để hệ ba viên gạch 2, 3, 4 nằm cân bằng thì hợp lực của chúng có giới hạn ngoài cùng của đường tác dụng chỉ có thể đi qua của mép phải của viên gạch 1 dưới cùng. Cũng bằng phép tính hợp lực, ta có thể xác định được khoảng cách nhô ra của viên 2 so với viên 1 là \({a_2} = {1 \over 6}L.\) Cuối cùng, trọng tâm của hệ 4 viên gạch cách mép bàn nhiều nhất chỉ có thể nằm trên đường thẳng đứng cách mép bàn một đoạn \({a_1} = {1 \over 8}L.\) (xem Hình 3.6G).
b) Vậy khoảng cách \(h = \left( {{1 \over 2} + {1 \over 4} + {1 \over 6} + {1 \over 8}} \right)L = {{25} \over {24}}L.\)