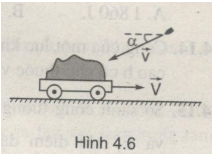
Một xe cát có khối lượng M đang chuyển động với vận tốc V trên mặt nằm ngang. Người ta bắn một viên đạn có khối lượng m vào xe với vận tốc v hợp với phương ngang một góc \(\alpha \) và ngược hướng chuyển động của xe (Hình 4.6). Bỏ qua ma sát giữa xe và mặt đường.
a)Tìm vận tốc u của xe sau khi đạn đã nằm yên trong cát.
b)Tính ngoại lực (hướng và độ lớn ) tác dụng lên hệ đạn- xe trong thời gian \(\Delta t\) xảy ra va chạm.

a)Xe chỉ chịu tác dụng của trọng lực \(\overrightarrow P \) và phản lực \(\overrightarrow N \) hướng vuông góc với mặt đường. Chọn hệ trục tọa độ xOy như Hình 4.1G.
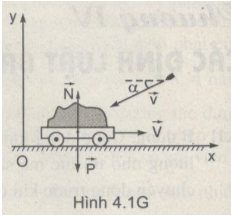
Theo phương ngang, tổng động lượng của hệ xe-đạn được bảo toàn vì không có ngoại lực tác dụng.
Chọn chiều dương là chiều chuyển động ban đầu của xe, ta viết được :
Advertisements (Quảng cáo)
\(\eqalign{ & MV - mv\cos \alpha = (M + m)u \cr & u = {{MV - mv\cos \alpha } \over {M + m}} \cr} \)
Vận tốc u của xe (có đạn nằm ở trong ) sau va chạm có phương ngang và chiều tùy thuộc dấu hiệu MV-mvcos\(\alpha \).
b)Giả thiết thời gian va chạm là \(\Delta t\). Theo phương y, động lượng của hệ xe-đạn sẽ biến thiên vì có ngoại lực tác dụng. Ta có đẳng thức về xung lượng của lực :
\(F.\Delta t = \Delta p\)
Từ đó : \((N - P)\Delta t = 0 - ( - mv\sin \alpha ) = mvsin\alpha \)
Suy ra \(N - P = {{mv\sin \alpha } \over {\Delta t}} > 0.\)
Kết quả trên cho biết N>P, tức là áp lực vuông góc của xe lên mặt đường lớn hơn trọng lượng của xe. Có thể nhận xét thêm : nếu bắn viên đạn theo phương ngang vào xe, tức là \(\sin \alpha = 0,\) thì ta lại có N=P.
