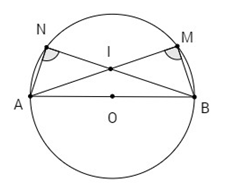
Bài 10. Cho hai điểm \(M, N\) nằm trên đường tròn đường kính \(AB = 2R\). Gọi \(I\) là giao điểm của hai đường thẳng \(AM, BN\).
a) Chứng minh rằng \(\overrightarrow {AM} .\overrightarrow {AI} = \overrightarrow {AB} .\overrightarrow {AI} \,\,;\,\,\overrightarrow {BN} .\overrightarrow {BI} = \overrightarrow {BA} .\overrightarrow {BI}.\)
b) Tính \(\overrightarrow {AM} .\overrightarrow {AI} + \,\,\overrightarrow {BN} .\overrightarrow {BI} \) theo \(R\).

Advertisements (Quảng cáo)
a) Ta có \(\overrightarrow {AM} .\,\overrightarrow {AI} = (\overrightarrow {AB} + \overrightarrow {BM} ).\,\overrightarrow {AI} = \overrightarrow {AB} .\,\overrightarrow {AI} + \overrightarrow {BM} .\,\overrightarrow {AI} = \overrightarrow {AB} .\,\overrightarrow {AI} \) ( vì \(\overrightarrow {BM} .\,\overrightarrow {AI} = 0\) ).
Tương tự, \(\overrightarrow {BN} .\,\overrightarrow {BI} = (\overrightarrow {BA} + \,\overrightarrow {AN} ).\,\overrightarrow {BI} = \overrightarrow {BA} .\,\overrightarrow {BI} + \overrightarrow {AN} .\,\overrightarrow {BI} = \overrightarrow {BA} .\,\overrightarrow {BI} \) ( vì \(\overrightarrow {AN} .\,\overrightarrow {BI} = 0\) ).
b) Theo câu a), \(\overrightarrow {AM} .\overrightarrow {AI} + \overrightarrow {BN} .\overrightarrow {BI} = \overrightarrow {AB} .\overrightarrow {AI} \, + \overrightarrow {BA} .\overrightarrow {BI} \)
\( = \overrightarrow {AB} (\overrightarrow {AI} - \overrightarrow {BI} ) = \overrightarrow {AB} .\,\overrightarrow {AB} = A{B^2} = 4{R^2}.\)
