Cho đường tròn (O; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau.
a) Chứng minh rằng \(A{B^2} + C{D^2}\) không đổi.
b) Chứng minh rằng \(P{A^2} + P{B^2} + P{C^2} + P{D^2}\) không phụ thuộc vào vị trí của điểm P.

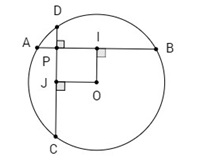
a) Gọi I, J lần lượt là trung điểm của AB, CD.
Ta có \(OI \bot AB\,\,;\,\,OJ \bot CD\)
Advertisements (Quảng cáo)
Suy ra OIPJ là hình chữ nhật. Ta có
\(\eqalign{
& A{B^2} + C{D^2} = 4(A{I^2} + C{J^2}) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 4(O{A^2} - O{I^2} + C{O^2} - J{O^2}) \cr} \)
\( = 4(2{R^2} - O{P^2})\) ( không đổi do cố định).
b) Ta có
\(\eqalign{
& P{A^2} + P{B^2} + P{C^2} + P{D^2} \cr&= {(\overrightarrow {PA} - \overrightarrow {PB} )^2} + {(\overrightarrow {PC} - \overrightarrow {PD} )^2} + 2.\overrightarrow {PA} .\,\overrightarrow {PB} + 2\overrightarrow {PC} .\,\overrightarrow {PD} \cr
& = A{B^2} + C{D^2} + 4(P{O^2} - {R^2}) \cr
& = 4(2{R^2} - O{P^2}) + 4(P{O^2} - {R^2}) \cr
& = 4{R^2} \cr} \)
Vậy \(P{A^2} + P{B^2} + P{C^2} + P{D^2}\) không phụ thuộc vào vị trí của điểm P.
