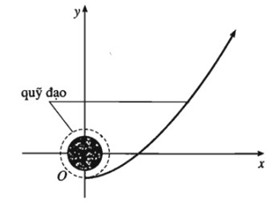
Khi một con tàu vũ trụ được phóng lên Mặt Trăng, trước hết nó sẽ bay vòng quanh Trái Đất. Sau đó, đến một thời điểm thích hợp, động cơ bắt đầu hoạt động đưa con tàu bay theo quỹ đạo là một nhánh hình parabol lên Mặt Trăng (trong hệ tọa độ Oxy như hình vẽ bên, X và y tính bằng nghìn kilômét). Biết rằng khi động cơ bắt đầu hoạt động, x= 0 thì y = -7. Sau đó y = -4 khi x = 10 và y = 5 khi x = 20.
a) Tìm hàm số có đồ thị là nhánh parabol nói trên
b) Theo lịch trình, đế đến được Mặt Trăng, con tàu phải đi qua điểm (100; V) với \(y = 294 ± 1,5\). Hỏi điều kiện đó có được thỏa màn hay không?
Đáp án
a) Gọi hàm bậc hai cần tìm là \(y = f(x) = ax^2 + bx + c\)
Theo đề bài ta có:
\(\left\{ \matrix{
f(0) = - 7 \hfill \cr
f(10) = - 4 \hfill \cr
f(20) = 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
c = - 7 \hfill \cr
100a + 10b + c = - 4 \hfill \cr
400a + 20b + c = 5 \hfill \cr} \right.\)
Advertisements (Quảng cáo)
\(\Leftrightarrow \left\{ \matrix{
a = 0,03 \hfill \cr
b = 0 \hfill \cr
c = - 7 \hfill \cr} \right.\)
Vậy: \(y = 0,03x^2– 7\)
b) Theo điều kiện khi \(x = 100\) thì \(y = 294 ± 1,5\)
Tức \(294 – 1,5 \le y \le 294 + 1,5\)
\(⇔ y ∈ [292,5; 295,5]\)
Ta có: \(f(100) = 0,03.100^2– 7 = 293\) (thỏa mãn điều kiện)
